10 conseils pour obtenir les meilleures réponses de l'IA
Craft AI vous livre ses secrets pour interroger votre IA de manière maîtrisée afin de révéler son plein potentiel.
An introduction to Causal Inference, why it is needed in data science and how Machine Learning can help, with real-world applications and exciting research directions.

In today’s data-driven world, understanding the underlying factors that drive outcomes is crucial for companies looking to optimize their services and customer experiences. Consider tech giants like Amazon, Spotify, Criteo or Netflix. These companies don’t just rely on observing what users do; they’re deeply invested in understanding why users behave the way they do.
For data scientists, this is where the concept of causal inference becomes indispensable. While traditional data analysis often focuses on identifying correlations, it’s the realm of causal inference that dives into the genuine cause-and-effect relationships. Being equipped with techniques of causal inference not only allows data scientists to draw more accurate conclusions but also empowers them to provide strategic insights that can guide impactful business decisions.
In essence, for forward-thinking companies and data professionals, causality is not just a theoretical concept but a critical tool that paves the way for meaningful actions and innovations. Absolutely! Let’s dive deeper into the first section, “Why correlation is not causation.”
In the realm of statistics and data science, a fundamental principle is understanding the difference between correlation and causation. While correlation indicates a relationship between two variables, causation goes a step further to show that a change in one variable directly results in a change in another. Some approaches, such as Granger causality[1], consider causality as a special case of correlation, in which A “causes” B if A is correlated with B and precedes it. However, in this article, we’ll stick to a more generalist definition of causality, a more ‘Pearlian’[2] approach, which is the one used in the field of causal inference, that consider causality as above and beyond correlation.
In particular, spurious correlations are correlations that might be statistically significant but are meaningless or misleading in practical terms. They arise due to either pure coincidence or a third, confounding variable.
For instance, imagine a video platform aiming to boost user engagement. Historically, they’ve observed two main types of users:
The platform, based on previous observations, decides to push the new recommendation system primarily to Infrequent Users because they have more room to increase their watch time.
After a few weeks, the platform decides to evaluate the impact of the recommendation system. The first, very simple approach is to compare the average watch time of users who received recommendations with those who didn’t. The results are shown in the bar plot below:

Surprise! It seems that the recommendation system has had a negative impact on watch time. But is this really the case? Let’s dig deeper. The platform decides to break down the results by user type, as shown in the bar plot below:

As we can see, the recommendation system has had a positive impact on both Frequent and Infrequent Users, but a seemingly negative impact overall. This is called Simpson’s Paradox, and is caused by a what we call a confounding variable.
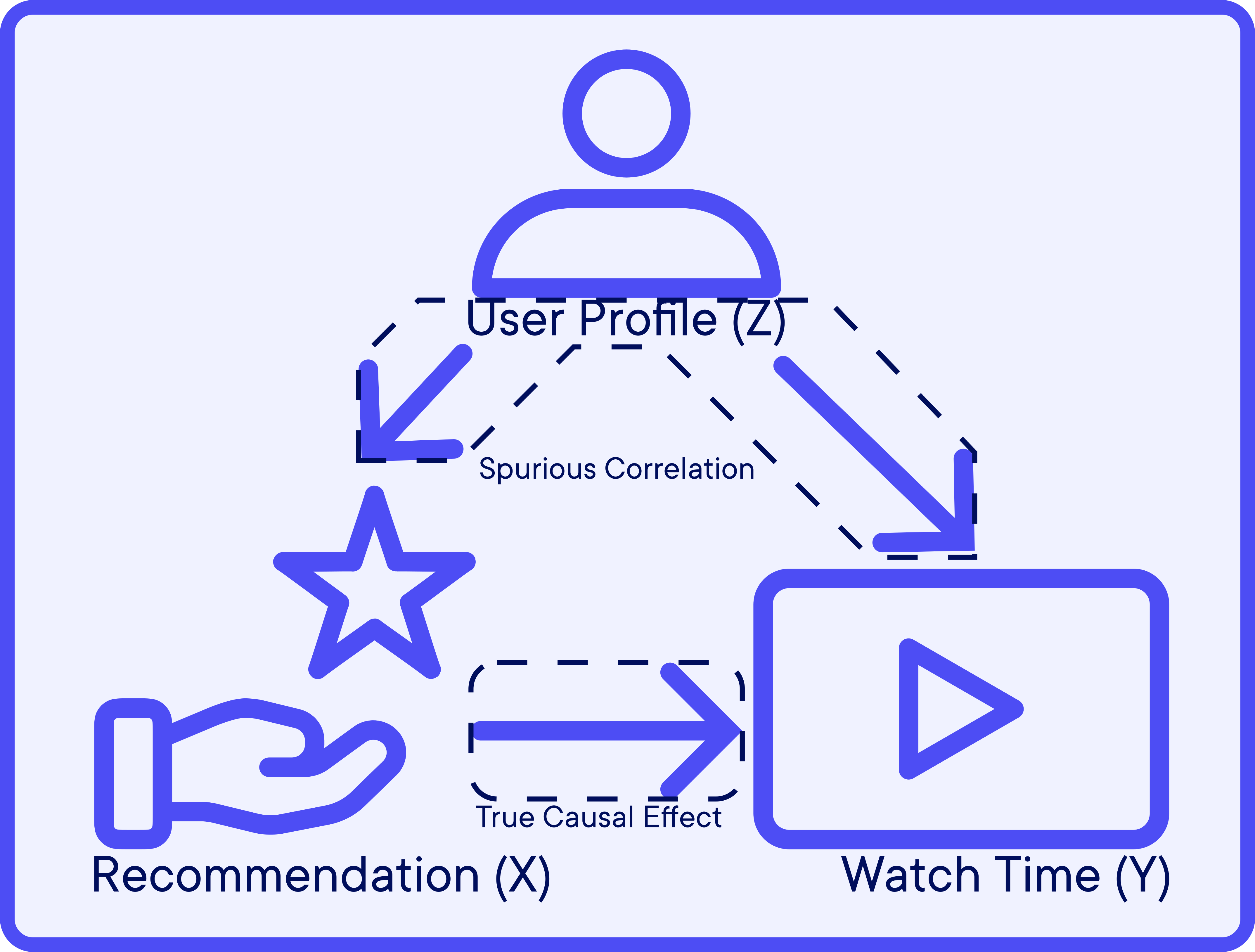
A confounding variable is an external factor that affects both the treatment (here, the recommendation)and the outcome (watch time). In this case, the confounding variable is the user type. We can represent this relationship in a causal graph, a type of graph that shows the causal relationships between variables:

On thing that is important to note is that what the platform really wants to know is not the correlation between the recommendation system and watch time, but the causal effect of the recommendation system on watch time. In other words, they want to know how much would watch time increase if they were to push the recommendation system to all users.
To model this intervention, Causal Inference provides us with to do-operator. Let us denote the recommendation system as X and the watch time as Y. Then, the first bar plot shows us P(Y|X), the observed distribution of the watch time given the recommendation system. However, as we pointed out, the platform is interested in P(Y|do(X = 1)), the distribution of the watch time if they were to push the recommendation system to all users. Here, both quantities are different because the confounding variable, the user type here, allows for spurious correlations between X and Y. Here, Infrequent Users are more likely to receive recommendations, and they also tend to watch less content. Thus, the observed distribution of Y given X is actually influenced in two ways, in a causal “direct” way, and in a “spurious” way through the user type.
Now, in this case, we know we need the do-operator to estimate the causal effect of the recommendation system on watch time, but we are yet to define the exact metric we are looking for. In this case, we are interested in the average treatment effect (ATE), which is the average effect of the recommendation system on watch time. Formally, we can define it as:
$$ATE = E[Y|do(X = 1)] − E[Y|do(X = 0)]$$
This metric is very useful to find the most beneficial treatment (or recommendation) overall, however, it does not tell us how the recommendation system affects each user type. To do so, we can define the conditional average treatment effect (CATE), which is the average effect of the recommendation system on watch time for each user type. Formally, we can define it as:
$$CATE(z) = E(Y_1 − Y_0|Z = z)$$
Where $Yi$ is the potential outcome under treatment $i$, and $Z$ is the user type. This metric is significantly harder to estimate, since, even if I can intervene on the system, I cannot observe both potential outcomes for the same user. In the example case where $Z$ is a binary user type, this is not too problematic because it essentially boils down to computing the $ATE$ for both group. For example, here, the second bar plot allows us to easily see that $CATE(\text{Frequent User}) = 5$ and $CATE(\text{Infrequent User}) = 20$. However, in more complex cases, where $Z$ might be several variables, this becomes much harder, since the condition $Z = z$ might refer to only a few users, and it can be really hard to observe both potential outcomes. This is why $CATE$ is not an interventional quantity, but a counterfactual one.
The gold standard for measuring $ATE$ is the randomized controlled trial (RCT), also called A/B testing. In RCTs, subjects are randomly assigned to different groups, which means the treatment (or recommendation) $X$ becomes fully random, effectively cuttings all paths from the confounding variable $Z$ to $X$. This means that the observed distribution of $Y$ given $X$ is now equal to the distribution of $Y$ given $do(X)$, getting rid of the spurious correlation, and thus, the $ATE$ can be estimated by comparing the average outcomes of the different groups.
However, RCTs are not always possible, and in many cases, we have to rely on observational data. In this case, we can use causal inference to estimate the $ATE$ and $CATE$. Causal inference is a field of statistics that aims to estimate causal effects from observational data.
A foundational tool to achieve this is the backdoor criterion, proposed by Judea Pearl. It is set of conditions used to identify variables that can be conditioned on to estimate causal effects from observational data. By “closing the backdoor” paths that could introduce bias, we can isolate the direct causal effect. Intuitively, it says we can estimate the causal effect of $X$ on $Y$ by conditioning on confounders. Formally, a set of variables $Z$ satisfies the backdoor criterion relative to $X$ and $Y$ if:
Then, is $Z$ satisfies this criterion, we can estimate the causal effect of $X$ on $Y$ by conditioning on $Z$:
$$P(Y|do(X)) = ∑_zP(Y|X, Z = z)P(Z = z)$$
Which means:
$$ATE = ∑_z(E[Y|X = 1, Z = z] − E[Y|X = 0, Z = z])P(Z = z)$$
Since
$$\begin{aligned}E[Y|do(X=i)] &= \sum_y y P(Y|do(X=i)) = \sum_y\sum_z y P(Y|do(X=i), Z=z)P(Z=z)\\&=\sum_z E[Y|do(X=i), Z=z] P(Z=z)\end{aligned}$$
In our previous recommendation example, since there are about as many Frequent Users as Infrequent Users, and we have
$$\begin{aligned}E[Y|X=1, Z=\text{Infrequent User}]=50\\E[Y|X=0, Z=\text{Infrequent User}]=30\\E[Y|X=1, Z=\text{Frequent User}]=105\\E[Y|X=0, Z=\text{Frequent User}]=100\\\end{aligned}$$
Therefore : $ATE = (105 − 100) × 0.5 + (50 − 30) × 0.5 = 12.5$.
However, in the real world, especially in complex scenarios like user behaviour on online platforms or intricate market dynamics, merely conditioning on confounders isn’t enough. There’s a vast sea of data, intricate interrelationships, and hidden variables. This is where we can blend the power of causal inference with another heavyweight in the data world: Machine Learning (ML).
First and foremost, sometimes, we do not have access to the full causal graph, and we have to learn it from the data. This is called Causal Discovery. The most straightforward way to do so is called the Peter-Clarck, or PC algorithm.
The PC algorithm is a prominent constraint-based method used for causal discovery from observational data. It seeks to identify the underlying causal graph that best represents the causal structure among a set of variables. The algorithm is based statistical independence tests to deduce the structure.
Basic Steps:
The PC algorithm, while simple in its foundation, provides a powerful tool for causal structure learning. By iteratively testing for conditional independencies and refining the graph structure, it offers a systematic approach to uncovering the intricate web of causal relationships from observational data.
However, the PC algorithm is not the only approach to causal discovery. There are also score-based methods, like the GES algorithm[4], or, recently, DAGMA[5](derived from NO TEARS [6]), there are also hybrid methods, like FCI[7].
Once we know the causal graph, and therefore the confounders,it is possible to use Meta-Learners, especially when the data are too complex to use the backdoor criterion directly. It is a family of approaches that aim to estimate causal effects from observational data. There are several approaches, we will be going throught the simplest here, the S-Learner, and the T-Learner.
S-Learner stands for Single Learner. It is the simplest approach, and it consists of training a single model to predict the outcome Y given the treatment X and the confounders Z.

Then, we can estimate the ATE by comparing the average predicted outcomes for each treatment.

In practice, this can be implemented quite simply using Uber’s CausalML library.
We can see it fits the empirical results quite well.
Another simple approach is the T-Learner. It stands for Two-Learners, it is similar to the S-Learner, but instead of training a single model, we train two models, one for each treatment group.

Then, we can estimate the ATE by comparing the average predicted outcomes for each treatment.
$τ(z) = μ_1(z) − μ_0(z)$
Similarly, it is pretty easy to estimate using CausalML.
But Causal Inference goes far beyond the simple examples displayed here, in meta-learners alone, there are a lot more models : X-Learner, DR-Learner, M-Learner, each with their own advantages and drawbacks. There are also other approaches, like causal forests, instrumental variables, and many more. All these tools are already used in a wide variety of domains in the real world.
Healthcare is a critical sector where decisions have direct implications on patient outcomes. The application of causal inference in this domain facilitates a more tailored approach to patient care. By understanding the causal relationships between treatments and outcomes, medical professionals can make decisions that are more aligned with individual patient needs.
Pharmaceutical companies also benefit from causal insights when developing new drugs. Analyzing causal relationships allows these companies to predict potential drug interactions and side effects, adding an additional dimension to the drug development process.
Additionally, by examining the causal factors associated with patient symptoms and disease progression, healthcare providers can anticipate potential complications, leading to early interventions and improved patient care.
The finance sector is characterized by its dynamic nature, with constant fluctuations and evolving trends. Investors are always seeking ways to optimize their decisions. By applying causal inference, they can move beyond merely observing market trends to understanding the underlying causes behind these movements. This deeper insight can lead to more strategic investment choices.
Financial institutions also find value in causal models for risk management. Predictive models that incorporate causal relationships can forecast events like loan defaults or potential financial downturns with greater accuracy.
Understanding consumer behavior is another area within finance where causality plays a role. Financial institutions can refine their product and service offerings based on insights into the causal factors that influence consumer choices.
Marketing strategies aim to influence consumer behavior and drive business outcomes. With causal inference, marketers can measure the actual impact of their campaigns more accurately. This allows them to differentiate the effects of a marketing initiative from other external factors.
Mapping customer journeys is an integral part of marketing. By analyzing the causal pathways that influence customer decisions, businesses can identify key touchpoints and optimize their marketing strategies accordingly.
Before introducing a new product or feature to the market, businesses can employ causal models to predict potential consumer responses. This predictive capability can inform product development and marketing strategies, ensuring alignment with market demand.
In each of these domains, the integration of causal inference methodologies enhances decision-making processes, offering a more comprehensive understanding of complex systems and relationships, but besides these real-world adoption, research in causal inference is also booming, with a lot of exciting new developments.
Reinforcement Learning (RL), where agents interact with environments aiming to maximize rewards, is a prime candidate for the integration of causal inference. Distinguishing between correlation and causation in observed rewards and actions can enhance agent policies. Especially in RL, an actual interventional distribution is practically accessible, emphasizing the importance of causality in such environments. Recognizing causal structures in complex RL scenarios can enhance decision-making and policy optimization[8].
Large Language Models (LLMs), exemplified by the likes of ChatGPT and LLaMA-2, are revolutionizing Natural Language Processing with their ability to produce human-like text. However, their intricate behaviors and vast parameter spaces necessitate a deeper understanding of their decision-making processes. Causal inference provides insights into why these models generate specific outputs. For tasks like fine-tuning, or when these models are deployed in real-world applications such as chatbots, understanding the causal underpinnings is crucial. Interestingly, LLMs can also play a role in causal inference itself. In scenarios where domain knowledge is essential, LLMs can potentially collaborate with human experts to deduce causal graphs or identify pertinent confounders[9,10].
Lastly, Generative Models stand out in their capacity to mimic data distributions. When these models are designed with causal structures in mind, they become causal generative models. They are then able to generate counterfactual and interventional data, offering a versatile approach to estimate causal effects, or any quantity relevant to the system at hand [11,12,13].
The importance of distinguishing between correlation and causation has become increasingly evident in the field of data science. Across diverse sectors, from healthcare to finance, and in advanced domains like reinforcement learning and large language models, the application of causal inference provides a deeper understanding of underlying systems and phenomena.
Incorporating causal methodologies into data-driven techniques allows for more precise interpretations and predictions. This integration is essential as the complexity of datasets and models continues to grow, ensuring that conclusions drawn are both accurate and meaningful.
As the field continues to evolve, the role of causal inference remains central, offering clarity and depth in an increasingly data-rich world.